Physics For Scientists And Engineers 6E - part 64

one  particle  is  that  from  the  other  particle  and  we  can  categorize this  as  a  situation  in
which Newton’s laws will be useful. If a force from particle 1 (for example, a gravitational
force) acts on particle 2, then there must be a second force—equal in magnitude but op-
posite  in  direction—that  particle  2  exerts  on  particle  1.  That  is,  they  form  a  Newton’s
third law action–reaction pair, so that 

F

12

! "

F

21

. We can express this condition as

Let  us  further  analyze this  situation  by  incorporating  Newton’s  second  law.  Over

some time interval, the interacting particles in the system will accelerate. Thus, replac-
ing each force with m

a gives

Now we replace the acceleration with its definition from Equation 4.5:

If  the  masses  m

1

and  m

2

are  constant,  we  can  bring  them  into  the  derivatives,  which

gives

(9.1)

To finalize this discussion, note that the derivative of the sum m

1

v

1

#

m

2

v

2

with respect

to time is zero. Consequently, this sum must be constant. We learn from this discussion
that the quantity m

v for a particle is important, in that the sum of these quantities for

an isolated system is conserved. We call this quantity linear momentum:

d

dt

 (m

1

v

1

#

m

2

v

2

) ! 0

d(m

1

v

1

)

dt

#

d(m

2

v

2

)

dt

!

0

m

1

 

d

v

1

dt

#

m

2

 

d

v

2

dt

!

0

 m

1

a

1

#

m

2

a

2

!

0

F

21

#

F

12

!

0

S E C T I O N   9 . 1 •  Linear Momentum and Its Conservation

253

v

2

m

2

m

1

F

21

F

12

v

1

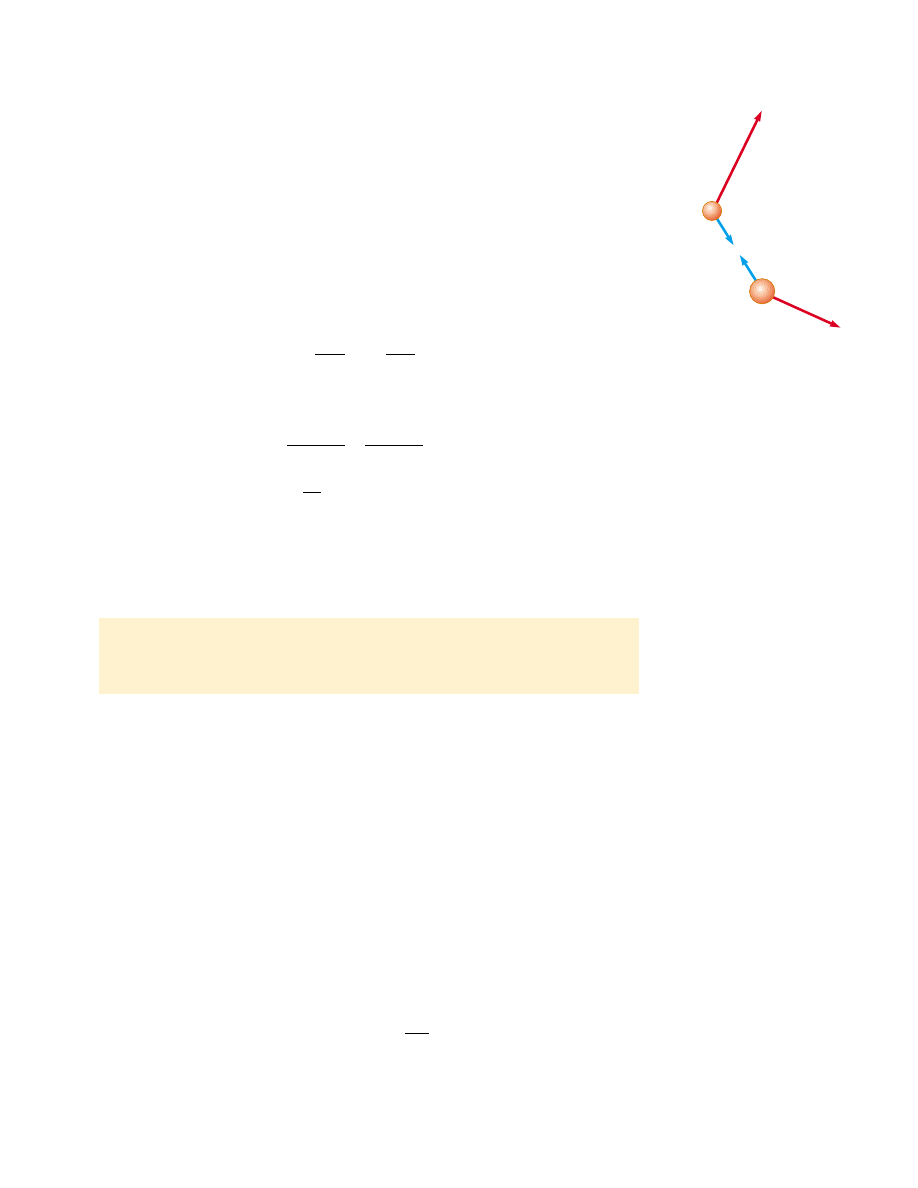
Figure 9.1 Two particles interact

with each other. According to

Newton’s third law, we must have

F

12

! "

F

21

.

The

linear momentum of a particle or an object that can be modeled as a particle of

mass m moving with a velocity 

v is defined to be the product of the mass and velocity:

(9.2)

p ! m v

Linear momentum is a vector quantity because it equals the product of a scalar quan-
tity m and a vector quantity 

v. Its direction is along v, it has dimensions ML/T, and its

SI unit is kg · m/s.

If a particle is moving in an arbitrary direction, 

p must have three components, and

Equation 9.2 is equivalent to the component equations

As you can see from its definition, the concept of momentum

1

provides a quantitative

distinction between heavy and light particles moving at the same velocity. For example,
the momentum of a bowling ball moving at 10 m/s is much greater than that of a ten-
nis  ball  moving  at  the  same  speed.  Newton  called  the  product  m

v  quantity  of  motion;

this is perhaps a more graphic description than our present-day word momentum, which
comes from the Latin word for movement.

Using Newton’s second law of motion, we can relate the linear momentum of a par-

ticle  to  the  resultant  force  acting  on  the  particle.  We  start  with  Newton’s  second  law
and substitute the definition of acceleration:

"

F ! ma ! m 

d

v

dt

p

x

!

mv

x

   

p

y

!

mv

y

   

p

z

!

mv

z

1

In this chapter, the terms momentum and linear momentum have the same meaning. Later, in Chapter 11,

we shall use the term angular momentum when dealing with rotational motion.

Definition of linear 

momentum of a particle

In Newton’s second law, the mass m is assumed to be constant. Thus, we can bring m
inside the derivative notation to give us

(9.3)

This shows that

the time rate of change of the linear momentum of a particle is

equal to the net force acting on the particle.

This  alternative  form  of  Newton’s  second  law  is  the  form  in  which  Newton  pre-

sented the law and is actually more general than the form we introduced in Chapter 5.
In addition to situations in which the velocity vector varies with time, we can use Equa-
tion 9.3 to study phenomena in which the mass changes. For example, the mass of a
rocket changes as fuel is burned and ejected from the rocket. We cannot use 

"

F ! ma

to analyze rocket propulsion; we must use Equation 9.3, as we will show in Section 9.7.

The real value of Equation 9.3 as a tool for analysis, however, arises if we apply it to

a system of two or more particles. As we have seen, this leads to a law of conservation of
momentum for an isolated system. Just as the law of conservation of energy is useful in
solving complex motion problems, the law of conservation of momentum can greatly
simplify the analysis of other types of complicated motion.

"

F !

d(m

v)

dt

!

d

p

dt

254

C H A P T E R   9 •  Linear Momentum and Collisions

Quick Quiz 9.1

Two objects have equal kinetic energies. How do the magni-

tudes of their momenta compare? (a) p

1

$

p

2

(b) p

1

!

p

2

(c) p

1

%

p

2

(d) not enough

information to tell.

Quick Quiz 9.2

Your physical education teacher throws a baseball to you at a

certain speed, and you catch it. The teacher is next going to throw you a medicine ball
whose mass is ten times the mass of the baseball. You are given the following choices:
You can have the medicine ball thrown with (a) the same speed as the baseball (b) the
same momentum (c) the same kinetic energy. Rank these choices from easiest to hard-
est to catch.

Using the definition of momentum, Equation 9.1 can be written

Because the time derivative of the total momentum 

p

tot

!

p

1

#

p

2

is zero, we conclude

that the total momentum of the system must remain constant:

(9.4)

or, equivalently,

(9.5)

where 

p

li

and 

p

2i

are the initial values and 

p

1f

and 

p

2f

the final values of the momenta

for the two particles for the time interval during which the particles interact. Equation
9.5 in component form demonstrates that the total momenta in the x, y, and z direc-
tions are all independently conserved:

(9.6)

This result, known as the 

law of conservation of linear momentum, can be extended

to any number of particles in an isolated system. It is considered one of the most im-
portant laws of mechanics. We can state it as follows:

p

ix

!

p

fx

   

p

iy

!

p

fy

   

p

iz

!

p

fz

p

1i

#

p

2i

!

p

1f

#

p

2f

p

tot

!

p

1

#

p

2

!

constant

d

dt

 (

p

1

#

p

2

) ! 0

▲

PITFALL PREVENTION

9.1 Momentum of a

System is Conserved

Remember  that  the  momentum
of an isolated system is conserved.
The  momentum  of  one  particle
within  an  isolated  system  is  not
necessarily  conserved,  because
other particles in the system may
be  interacting  with  it.  Always  ap-
ply  conservation  of  momentum
to an isolated system.

Newton’s second law for a

particle

This law tells us that 

the total momentum of an isolated system at all times equals

its initial momentum.

Notice that we have made no statement concerning the nature of the forces acting

on the particles of the system. The only requirement is that the forces must be internal
to the system.

S E C T I O N   9 . 1 •  Linear Momentum and Its Conservation

255

Whenever two or more particles in an isolated system interact, the total momentum
of the system remains constant.

Quick Quiz 9.3

A ball is released and falls toward the ground with no air re-

sistance. The isolated system for which momentum is conserved is (a) the ball (b) the
Earth (c) the ball and the Earth (d) impossible to determine.

Quick Quiz 9.4

A car and a large truck traveling at the same speed make a

head-on  collision  and  stick  together.  Which  vehicle  experiences  the  larger  change  in
the magnitude of momentum? (a) the car (b) the truck (c) The change in the magni-
tude of momentum is the same for both. (d) impossible to determine.

Example 9.1 The Archer

Let us consider the situation proposed at the beginning of
this section. A 60-kg archer stands at rest on frictionless ice
and  fires  a  0.50-kg  arrow  horizontally  at  50 m/s  (Fig.  9.2).
With what velocity does the archer move across the ice after
firing the arrow?

Solution We  cannot solve  this  problem  using  Newton’s  sec-
ond  law, 

"F ! ma, because  we  have  no  information  about

the force on the arrow or its acceleration. We cannot solve this
problem using an energy approach because we do not know
how much work is done in pulling the bow back or how much
potential energy is stored in the bow. However, we can solve
this problem very easily with conservation of momentum.

Let us take the system to consist of the archer (including

the bow) and the arrow. The system is not isolated because
the gravitational force and the normal force act on the sys-
tem. However, these forces are vertical and perpendicular to
the motion of the system. Therefore, there are no external
forces in the horizontal direction, and we can consider the
system to be isolated in terms of momentum components in
this direction.

The total horizontal momentum of the system before the

arrow is fired is zero (m

1

v

1i

#

m

2

v

2i

!

0), where the archer is

particle 1 and the arrow is particle 2. Therefore, the total hori-
zontal momentum after the arrow is fired must be zero; that is,

We choose the direction of firing of the arrow as the positive x
direction. With m

1

!

60 kg, m

2

!

0.50 kg, and 

v

2f

!

50

iˆ m/s,

solving for 

v

1f

, we find the recoil velocity of the archer to be

The negative sign for 

v

1f

indicates that the archer is moving

to the left after the arrow is fired, in the direction opposite

"

0.42

iˆ  m/s

v

1f

! "

m

2

m

1

 

 

v

2f

! "

#

0.50 kg

60 kg

$

 (50

iˆ  m/s) !

 m

1

v

1f

#

m

2

v

2f

!

0

the  direction  of  motion  of  the  arrow,  in  accordance  with
Newton’s third law. Because the archer is much more mas-
sive than the arrow, his acceleration and consequent velocity
are much smaller than the acceleration and velocity of the
arrow.

What  If?

What  if  the  arrow  were  shot  in  a  direction  that

makes an angle 

&

with the horizontal? How will this change

the recoil velocity of the archer?

Answer The  recoil  velocity  should  decrease  in  magnitude
because only a component of the velocity is in the x direction.

Figure 9.2 (Example 9.1) An archer fires an arrow horizontally

to the right. Because he is standing on frictionless ice, he will

begin to slide to the left across the ice.

Interactive

Conservation of momentum

9.2 Impulse and Momentum

According to Equation 9.3, the momentum of a particle changes if a net force acts on
the particle. Knowing the change in momentum caused by a force is useful in solving
some types of problems. To build a better understanding of this important concept, let
us assume that a single force 

F acts on a particle and that this force may vary with time.

According to Newton’s second law, 

F ! d p/dt, or

(9.7)

We can integrate

2

this expression to find the change in the momentum of a particle

when the force acts over some time interval. If the momentum of the particle changes
from 

p

i

at time t

i

to 

p

f

at time t

f

, integrating Equation 9.7 gives

d

p ! Fdt

256

C H A P T E R   9 •  Linear Momentum and Collisions

If the arrow were shot straight up, for example, there would
be  no  recoil  at  all—the  archer  would  just  be  pressed  down
into the ice because of the firing of the arrow.

Only  the  x component  of  the  momentum  of  the  arrow

should be used in a conservation of momentum statement,
because momentum is only conserved in the x direction. In
the y direction, the normal force from the ice and the gravi-
tational force are external influences on the system. Conser-
vation of momentum in the x direction gives us

m

1

v

1f

#

m

2

v

2f

   

 

cos & ! 0

leading to

For & ! 0, cos & ! 1 and this reduces to the value when the
arrow is fired horizontally. For nonzero values of &, the co-
sine function is less than 1 and the recoil velocity is less than
the  value  calculated  for  & ! 0.  If  & ! 90°,  cos & ! 0,  and
there is no recoil velocity v

1f

, as we argued conceptually.

v

1f

! "

m

2

m

1

 v

2f  

cos &

At the Interactive Worked Example link at http://www.pse6.com, you can change the mass of the archer and the mass and
speed of the arrow.

Example 9.2 Breakup of a Kaon at Rest

An important point to learn from this problem is that even
though  it  deals  with  objects  that  are  very  different  from
those  in  the  preceding  example,  the  physics  is  identical: 
linear momentum is conserved in an isolated system.

p

#

! "

p

"

One  type  of  nuclear  particle,  called  the  neutral  kaon (K

0

),

breaks up into a pair of other particles called pions ('

#

and

'

"

) that are oppositely charged but equal in mass, as illus-

trated  in  Figure  9.3.  Assuming  the  kaon  is  initially  at  rest,
prove that the two pions must have momenta that are equal
in magnitude and opposite in direction.

Solution The breakup of the kaon can be written

If we let 

p

#

be the final momentum of the positive pion and

p

"

the final momentum of the negative pion, the final mo-

mentum  of  the  system  consisting  of  the  two  pions  can  be
written

Because the kaon is at rest before the breakup, we know that

p

i

!

0. Because the momentum of the isolated system (the

kaon  before  the  breakup,  the  two  pions  afterward)  is 
conserved, 

p

i

!

p

f

!

0, so that 

p

#

#

p

"

!

0, or

p

f

!

p

#

#

p

"

K

0

9: '

#

#

'

"

Κ

Before

decay

(at rest)

p

+

p

–

π

–

π

+

After decay

π

π

0

Figure 9.3 (Example 9.2) A kaon at rest breaks up sponta-

neously into a pair of oppositely charged pions. The pions move

apart with momenta that are equal in magnitude but opposite

in direction.

2

Note  that  here  we  are  integrating  force  with  respect  to  time.  Compare  this  with  our  efforts  in

Chapter 7, where we integrated force with respect to position to find the work done by the force.