Physics For Scientists And Engineers 6E - part 45
59.
The pilot of an airplane executes a constant-speed loop-the-
loop maneuver in a vertical circle. The speed of the airplane
is 300 mi/h, and the radius of the circle is 1 200 ft. (a) What
is the pilot’s apparent weight at the lowest point if his true
weight is 160 lb? (b) What is his apparent weight at the
highest point? (c) What If? Describe how the pilot could ex-
perience weightlessness if both the radius and the speed can
be varied. (Note: His apparent weight is equal to the magni-
tude of the force exerted by the seat on his body.)
60.
A penny of mass 3.10 g rests on a small 20.0-g block sup-
ported by a spinning disk (Fig. P6.60). The coefficients of
friction between block and disk are 0.750 (static) and
above the horizontal. If the radius of the tub is 0.330 m,
what rate of revolution is needed?
51. We will study the most important work of Nobel laureate
Arthur Compton in Chapter 40. Disturbed by speeding
cars outside the physics building at Washington University
in St. Louis, Compton designed a speed bump and had it
installed. Suppose that a 1 800-kg car passes over a bump
in a roadway that follows the arc of a circle of radius
20.4 m as in Figure P6.51. (a) What force does the road ex-
ert on the car as the car passes the highest point of the
bump if the car travels at 30.0 km/h? (b) What If? What is
the maximum speed the car can have as it passes this high-
est point without losing contact with the road?
52.
A car of mass m passes over a bump in a road that follows
the arc of a circle of radius R as in Figure P6.51. (a) What
force does the road exert on the car as the car passes the
highest point of the bump if the car travels at a speed v?
(b) What If? What is the maximum speed the car can have
as it passes this highest point without losing contact with
the road?
53.
Interpret the graph in Figure 6.18(b). Proceed as follows:
(a) Find the slope of the straight line, including its units.
(b) From Equation 6.6,
, identify the theoreti-
cal slope of a graph of resistive force versus squared speed.
(c) Set the experimental and theoretical slopes equal to
each other and proceed to calculate the drag coefficient of
the filters. Use the value for the density of air listed on the
book’s endpapers. Model the cross-sectional area of the fil-
ters as that of a circle of radius 10.5 cm. (d) Arbitrarily
choose the eighth data point on the graph and find its ver-
tical separation from the line of best fit. Express this scat-
ter as a percentage. (e) In a short paragraph state what the
graph demonstrates and compare it to the theoretical pre-
diction. You will need to make reference to the quantities
plotted on the axes, to the shape of the graph line, to the
data points, and to the results of parts (c) and (d).
54.
A student builds and calibrates an accelerometer, which
she uses to determine the speed of her car around a cer-
tain unbanked highway curve. The accelerometer is a
plumb bob with a protractor that she attaches to the roof
of her car. A friend riding in the car with her observes that
the plumb bob hangs at an angle of 15.0° from the vertical
when the car has a speed of 23.0 m/s. (a) What is the cen-
tripetal acceleration of the car rounding the curve?
(b) What is the radius of the curve? (c) What is the speed
of the car if the plumb bob deflection is 9.00° while round-
ing the same curve?
55.
Suppose the boxcar of Figure 6.13 is moving with constant
acceleration a up a hill that makes an angle 1 with the
R !
1
2
D-Av
2
horizontal. If the pendulum makes a constant angle " with
the perpendicular to the ceiling, what is a?
56.
(a) A luggage carousel at an airport has the form of a sec-
tion of a large cone, steadily rotating about its vertical axis.
Its metallic surface slopes downward toward the outside,
making an angle of 20.0° with the horizontal. A piece of
luggage having mass 30.0 kg is placed on the carousel,
7.46 m from the axis of rotation. The travel bag goes
around once in 38.0 s. Calculate the force of static friction
between the bag and the carousel. (b) The drive motor is
shifted to turn the carousel at a higher constant rate of
rotation, and the piece of luggage is bumped to another
position, 7.94 m from the axis of rotation. Now going
around once in every 34.0 s, the bag is on the verge of slip-
ping. Calculate the coefficient of static friction between
the bag and the carousel.
Because the Earth rotates about its axis, a point on
the equator experiences a centripetal acceleration of
0.033 7 m/s
2
, while a point at the poles experiences no
centripetal acceleration. (a) Show that at the equator the
gravitational force on an object must exceed the normal
force required to support the object. That is, show that the
object’s true weight exceeds its apparent weight. (b) What
is the apparent weight at the equator and at the poles of a
person having a mass of 75.0 kg? (Assume the Earth is a
uniform sphere and take g ! 9.800 m/s
2
.)
58.
An air puck of mass m
1
is tied to a string and allowed to re-
volve in a circle of radius R on a frictionless horizontal
table. The other end of the string passes through a hole in
the center of the table, and a counterweight of mass m
2
is
tied to it (Fig. P6.58). The suspended object remains in
equilibrium while the puck on the tabletop revolves. What
is (a) the tension in the string? (b) the radial force acting
on the puck? (c) the speed of the puck?
57.
Problems
177
m
1
R
m
2
Figure P6.58
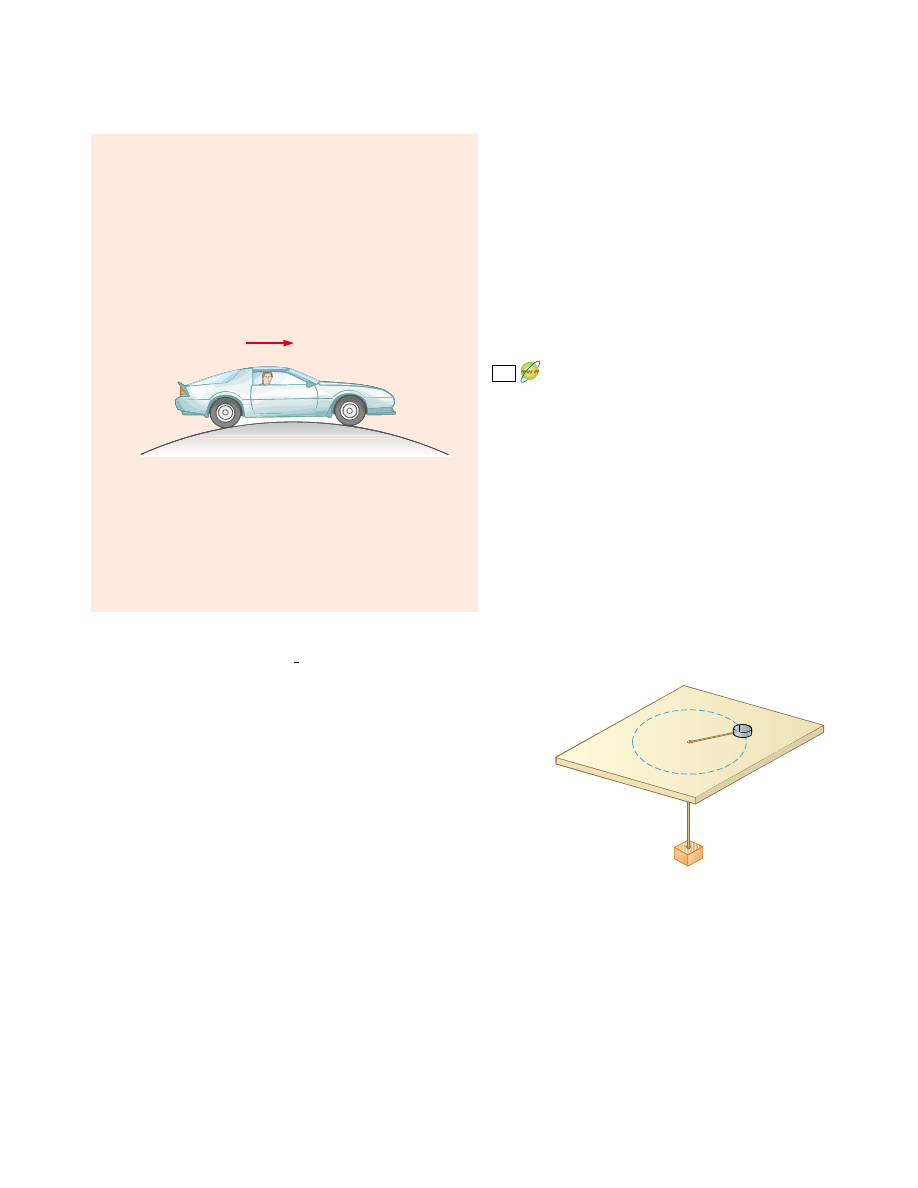
v
Figure P6.51 Problems 51 and 52.