Physics For Scientists And Engineers 6E - part 22

S E C T I O N   4 . 3 •  Projectile Motion

85

(1)

constant-velocity motion in the horizontal direction and (2) free-fall motion

in  the  vertical  direction.  The  horizontal  and  vertical  components  of  a  projectile’s
motion are completely independent of each other and can be handled separately, with
time t as the common variable for both components.

Quick Quiz 4.3

Suppose you are running at constant velocity and you wish

to  throw  a  ball  such  that  you  will  catch  it  as  it  comes  back  down.  In  what  direction
should you throw the ball relative to you? (a) straight up (b) at an angle to the ground
that depends on your running speed (c) in the forward direction.

Quick  Quiz  4.4

As  a  projectile  thrown  upward  moves  in  its  parabolic  path

(such as in Figure 4.8), at what point along its path are the velocity and acceleration
vectors  for  the  projectile  perpendicular  to  each  other?  (a)  nowhere  (b)  the  highest
point (c) the launch point.

Quick Quiz 4.5

As the projectile in Quick Quiz 4.4 moves along its path, at

what point are the velocity and acceleration vectors for the projectile parallel to each
other? (a) nowhere (b) the highest point (c) the launch point.

Example 4.2 Approximating Projectile Motion

A ball is thrown in such a way that its initial vertical and hor-
izontal  components  of  velocity  are  40 m/s  and  20 m/s,  re-
spectively. Estimate the total time of flight and the distance
the ball is from its starting point when it lands.

Solution A motion diagram like Figure 4.9 helps us concep-
tualize the problem. The phrase “A ball is thrown” allows us
to  categorize this  as  a  projectile  motion  problem,  which  we
analyze by  continuing  to  study  Figure  4.9.  The  acceleration
vectors  are  all  the  same,  pointing  downward  with  a  magni-
tude  of  nearly  10 m/s

2

.  The  velocity  vectors  change  direc-

tion. Their horizontal components are all the same: 20 m/s. 

Remember that the two velocity components are inde-

pendent of each other. By considering the vertical motion

Figure 4.9 (Example 4.2) Motion diagram for a projectile.

r

f

x

(x, y)

gt

2

v

i

t

O

y

1

2

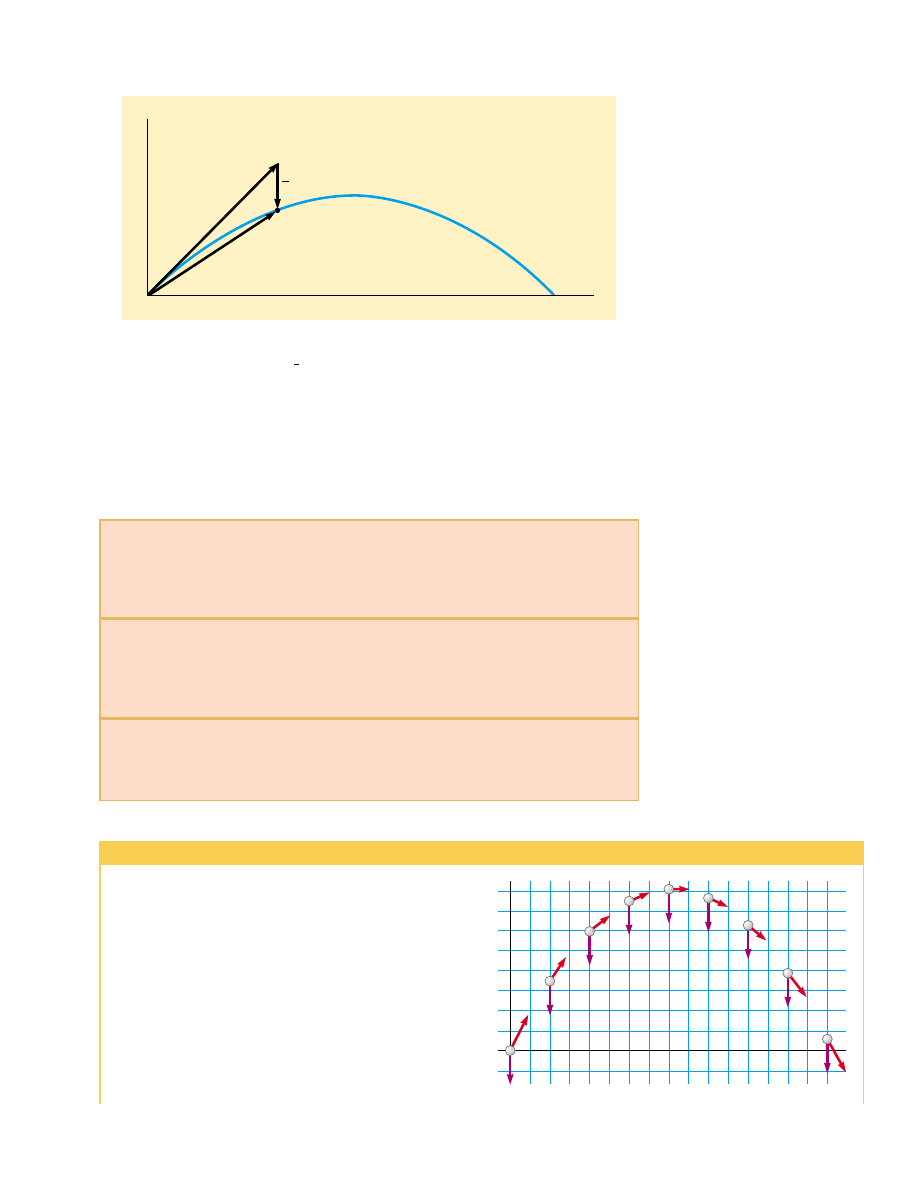
Figure 4.8 The position vector r

f

of a projectile launched from the origin whose initial

velocity at the origin is v

i

. The vector v

i

t would be the displacement of the projectile if

gravity were absent, and the vector 

is its vertical displacement due to its downward

gravitational acceleration.

1

2

 

gt

 

2

86

C H A P T E R   4 •  Motion in Two Dimensions

Horizontal Range and Maximum Height of a Projectile

Let us assume that a projectile is launched from the origin at t

i

"

0 with a positive v

yi

component, as shown in Figure 4.10. Two points are especially interesting to analyze:
the peak point !, which has Cartesian coordinates (R/2, h), and the point ", which
has  coordinates  (R, 0).  The  distance  R is  called  the  horizontal  range of  the  projectile,
and the distance h is its maximum height. Let us find h and R in terms of v

i

, '

i

, and g.

We  can  determine  h by  noting  that  at  the  peak, 

Therefore,  we  can  use

Equation 4.8a to determine the time t

A

at which the projectile reaches the peak:

Substituting  this  expression  for  t

A

into  the  y part  of  Equation  4.9a  and  replacing

y " y

A

with h, we obtain an expression for h in terms of the magnitude and direction of

the initial velocity vector: 

(4.13)

The  range  R is  the  horizontal  position  of  the  projectile  at  a  time  that  is  twice

the time at which it reaches its peak, that is, at time t

B

"

2t

A

. Using the x part of Equa-

tion 4.9a, noting that v

xi

"

v

x

B

"

v

i

cos '

i

and setting x

B

"

R at t " 2t

A

, we find that

Using  the  identity  sin  2' " 2sin ' cos ' (see  Appendix  B.4),  we  write 

R in  the  more

compact form

(4.14)

The maximum value of R from Equation 4.14 is R

max

"

v

i

2

/g. This result follows

from  the  fact  that  the  maximum  value  of  sin  2'

i

is  1,  which  occurs  when  2'

i

"

90°.

Therefore, R is a maximum when '

i

"

45°.

Figure 4.11 illustrates various trajectories for a projectile having a given initial speed

but launched at different angles. As you can see, the range is a maximum for '

i

"

45°.

In addition, for any '

i

other than 45°, a point having Cartesian coordinates (R, 0) can be

reached by using either one of two complementary values of '

i

, such as 75° and 15°. Of

course, the maximum height and time of flight for one of these values of '

i

are different

from the maximum height and time of flight for the complementary value.

R "

v

2

i  

  

 

sin 2'

i

g

"

(v

i  

cos '

i

)

2v

i 

 

sin '

i

g

"

2v

2

i    

sin '

i 

 

cos '

i

g

R " v

xi

t

B

"

(v

i  

cos '

i

)2t

A

h "

v

2

i   

 

sin

2

 '

i

2g

h " (v

i 

 

sin '

i

)

v

i 

 

sin '

i

g

#

1

2

g

#

v

i

 

 

sin '

i

g

$

2

t

A

"

v

i  

sin '

i

g

0 " v

i

 sin '

i

#

gt

A

v

yf

"

v

yi

&

a

y

t

v

y

A

"

0.

first,  we  can  determine  how  long  the  ball  remains  in  the
air.  Because  the  vertical  motion  is  free-fall,  the  vertical
components  of  the  velocity  vectors  change,  second  by
second, from 40 m/s to roughly 30, 20, and 10 m/s in the
upward direction, and then to 0 m/s. Subsequently, its ve-
locity becomes 10, 20, 30, and 40 m/s in the downward di-
rection.  Thus  it  takes  the  ball  about  4 s  to  go  up  and
another 4 s to come back down, for a total time of flight of
approximately 8 s.

Now we shift our analysis to the horizontal motion. Be-

cause  the  horizontal  component  of  velocity  is  20 m/s,  and
because  the  ball  travels  at  this  speed  for  8 s,  it  ends  up  ap-
proximately 160 m from its starting point.

This is the first example that we have performed for pro-

jectile  motion.  In  subsequent  projectile  motion  problems,
keep in mind the importance of separating the two compo-
nents and of making approximations to give you rough ex-
pected results.

R

x

y

h

v

i

v

y

A

 = 0

!

"

θ

i

O

Figure 4.10 A projectile launched

from the origin at t

i

"

0 with an

initial velocity v

i

. The maximum

height of the projectile is h, and

the horizontal range is R. At !, the

peak of the trajectory, the particle

has coordinates (R/2, h).

▲

PITFALL PREVENTION

4.3 The Height and Range

Equations

Equation 4.14 is useful for calcu-
lating  R only  for  a  symmetric
path,  as  shown  in  Figure  4.10.  If
the path is not symmetric, do not
use  this  equation.  The  general  ex-
pressions  given  by  Equations  4.8
and 4.9 are the more important re-
sults,  because  they  give  the  posi-
tion  and  velocity  components  of
any particle  moving  in  two  di-
mensions at any time t.

S E C T I O N   4 . 3 •  Projectile Motion

87

x(m)

50

100

150

y(m)

75

°

60

°

45

°

30

°

15

°

v

i

 = 50 m/s

50

100

150

200

250

Active Figure 4.11 A projectile launched from the origin with an initial speed of

50 m/s at various angles of projection. Note that complementary values of 

'

i

result in

the same value of R (range of the projectile).

P R O B L E M - S O LV I N G   H I N T S

Projectile Motion

We suggest that you use the following approach to solving projectile motion
problems:

•

Select a coordinate system and resolve the initial velocity vector into x and y
components.

•

Follow the techniques for solving constant-velocity problems to analyze the hori-
zontal motion. Follow the techniques for solving constant-acceleration problems
to analyze the vertical motion. The x and y motions share the same time t.

Example 4.3 The Long Jump

A long-jumper (Fig. 4.12) leaves the ground at an angle of
20.0° above the horizontal and at a speed of 11.0 m/s.

(A)

How far does he jump in the horizontal direction? (As-

sume his motion is equivalent to that of a particle.)

Solution We  conceptualize the  motion  of  the  long-jumper
as equivalent to that of a simple projectile such as the ball
in Example 4.2, and categorize this problem as a projectile
motion problem. Because the initial speed and launch an-
gle are given, and because the final height is the same as
the  initial  height,  we  further  categorize  this  problem  as
satisfying  the  conditions  for  which  Equations  4.13  and
4.14 can be used. This is the most direct way to analyze this
problem, although the general methods that we have been
describing will always give the correct answer. We will take
the  general  approach  and  use  components.  Figure  4.10

Quick Quiz 4.6

Rank the launch angles for the five paths in Figure 4.11 with

respect to time of flight, from the shortest time of flight to the longest.

provides  a  graphical  representation  of  the  flight  of  the
long-jumper. As before, we set our origin of coordinates at
the takeoff point and label the peak as ! and the landing
point  as  ".  The  horizontal  motion  is  described  by  Equa-
tion 4.11:

The value of x

B

can be found if the time of landing t

B

is

known. We can find t

B

by remembering that a

y

" #

g and by

using the y part of Equation 4.8a. We also note that at the top
of the jump the vertical component of velocity v

y

A

is zero:

t

A

"

0.384 s

0 " (11.0 m/s)

 

sin 20.0) # (9.80 m/s

2

)t

A

v

yf

"

v

y

A

"

v

i

  

 

sin '

i

#

gt

A

x

f

"

x

B

"

(v

i

 

 

cos '

i

)t

B

"

(11.0 m/s)(cos 20.0))t

B

At the Active Figures link at

http://www.pse6.com, you can

vary the projection angle to ob-

serve the effect on the trajectory

and measure the flight time.

Figure 4.12 (Example 4.3) Mike Powell, current holder of the

world long jump record of 8.95 m. 

Mike Powell/Allsport/Getty Images

another  0.384 s  passes  before  the  jumper  returns  to  the
ground.  Therefore,  the  time  at  which  the  jumper  lands  is
t

B

"

2t

A

"

0.768 s. Substituting this value into the above ex-

pression for x

f

gives

This is a reasonable distance for a world-class athlete.

(B)

What is the maximum height reached?

Solution We  find  the  maximum  height  reached  by  using
Equation 4.12:

To  finalize this  problem,  find  the  answers  to  parts  (A)  and
(B) using Equations 4.13 and 4.14. The results should agree.
Treating  the  long-jumper  as  a  particle  is  an  oversimplifica-
tion.  Nevertheless,  the  values  obtained  are  consistent  with
experience in sports. We learn that we can model a compli-
cated system such as a long-jumper as a particle and still ob-
tain results that are reasonable.

0.722 m

#

1

2

(9.80 m/s

2

)(0.384 s)

2

"

"

(11.0 m/s)(sin 20.0))(0.384 s)

y

max

"

y

A

"

(v

i

  

 

sin '

i

)t

A

#

1

2

gt

A

2

7.94 m

x

f

"

x

B

"

(11.0 m/s)(cos 20.0))(0.768 s) "

88

C H A P T E R   4 •  Motion in Two Dimensions

Example 4.4 A Bull’s-Eye Every Time

In a popular lecture demonstration, a projectile is fired at a
target T in such a way that the projectile leaves the gun at
the same time the target is dropped from rest, as shown in
Figure 4.13. Show that if the gun is initially aimed at the sta-
tionary target, the projectile hits the target.

Solution Conceptualize the problem by studying Figure 4.13.
Notice that the problem asks for no numbers. The expected
result must involve an algebraic argument. Because both ob-
jects are subject only to gravity, we categorize this problem as

one involving two objects in free-fall, one moving in one di-
mension  and  one  moving  in  two.  Let  us  now  analyze the
problem. A collision results under the conditions stated by
noting that, as soon as they are released, the projectile and
the  target  experience  the  same  acceleration,  a

y

" #

g.  Fig-

ure 4.13b shows that the initial y coordinate of the target is
x

T

tan '

i

and that it falls to a position  gt

2

below this coordi-

nate  at  time  t.  Therefore,  the  y coordinate  of  the  target  at
any moment after release is

y

T

"

x

T

  

tan '

i

#

1

2

gt

2

1

2

(a)

1

2

Target

Line of sight

y

x

Point of

collision

gt

 

2

x

T

 tan 

θ

i

y

T

Gun

0

x

T

θ

i

θ

(b)

Figure 4.13 (Example 4.4) (a) Multiflash photograph of projectile–target demonstra-

tion. If the gun is aimed directly at the target and is fired at the same instant the target

begins to fall, the projectile will hit the target. Note that the velocity of the projectile (red

arrows) changes in direction and magnitude, while its downward acceleration (violet

arrows) remains constant. (b) Schematic diagram of the projectile–target demonstration.

Both projectile and target have fallen through the same vertical distance at time t,

because both experience the same acceleration a

y

" #

g.

Interactive

Central Scientific Company

This is the time at which the long-jumper is at the top of

the  jump.  Because  of  the  symmetry  of  the  vertical  motion,