Physics For Scientists And Engineers 6E - part 59

SECTION 8.4 •  Changes in Mechanical Energy for Nonconservative Forces

233

!

E

mech

" #

f

k

d,  where  d is  the  horizontal  distance  trav-

eled by the skier.

To  find  the  distance  the  skier  travels  before  coming  to

rest,  we  take  K

C

"

0.  With  v

B

"

19.8 m/s  and  the  friction

force given by f

k

"

)

k

n " )

k

mg, we obtain

!

E

mech

"

E

C

#

E

B

" #

 

)

k

mgd

95.2 m

d "

v

 

B

 

2

2)

k

 

g

"

(19.8 m/s)

2

2(0.210)(9.80 m/s

2

)

"

" #

 

)

k

mgd

(K

C

%

U

C

) # (K

B

%

U

B

) " (0 % 0) #  (

1

2

mv

2

B

%

0)

Example 8.9 Block–Spring Collision

A  block  having  a  mass  of  0.80 kg  is  given  an  initial  velocity
v

A

"

1.2 m/s to the right and collides with a spring of negli-

gible  mass  and  force  constant  k " 50 N/m,  as  shown  in
Figure 8.14.

(A)

Assuming  the  surface  to  be  frictionless,  calculate  the

maximum compression of the spring after the collision.

Solution Our system in this example consists of the block
and  spring.  All  motion  takes  place  in  a  horizontal  plane,
so we do not need to consider changes in gravitational po-
tential  energy.  Before  the  collision,  when  the  block  is  at
!

,  it  has  kinetic  energy  and  the  spring  is  uncompressed,

so the elastic potential energy stored in the spring is zero.
Thus,  the  total  mechanical  energy  of  the  system  before
the  collision  is  just

.  After  the  collision,  when  the

block  is  at  #,  the  spring  is  fully  compressed;  now  the
block  is  at  rest  and  so  has  zero  kinetic  energy,  while  the
energy  stored  in  the  spring  has  its  maximum  value

1

2

mv

A

2

,  where  the  origin  of  coordinates x " 0  is 

chosen  to  be  the  equilibrium  position  of  the  spring  and
x

max

is  the  maximum  compression  of  the  spring,  which  in

this case happens to be x

C

. The total mechanical energy of

the  system  is  conserved  because  no  nonconservative  forces
act on objects within the system.

Because  the  mechanical  energy  of  the  system  is  con-

served, the kinetic energy of the block before the collision
equals  the  maximum  potential  energy  stored  in  the  fully
compressed spring:

"

(B)

Suppose  a  constant  force  of  kinetic  friction  acts  be-

tween  the  block  and  the  surface,  with  )

k

"

0.50.  If  the

speed of the block at the moment it collides with the spring
is  v

A

"

1.2 m/s,  what  is  the  maximum  compression  x

C

in

the spring?

Solution In this case, the mechanical energy of the system
is  not conserved  because  a  friction  force  acts  on  the  block.
The magnitude of the friction force is

Therefore, the change in the mechanical energy of the system
due to friction as the block is displaced from the equilibrium
position of the spring (where we have set our origin) to x

C

is

Substituting this into Equation 8.14 gives

Solving  the  quadratic  equation  for  x

C

gives  x

C

"

0.092 m

and  x

C

" #

0.25 m.  The  physically  meaningful  root  is 

x

C

"

0.092 m. The negative root does not apply to this sit-

uation because the block must be to the right of the origin
(positive  value  of  x)  when  it  comes  to  rest.  Note  that  the
value  of  0.092 m  is  less  than  the  distance  obtained  in  the
frictionless  case  of  part  (A).  This  result  is  what  we  expect
because friction retards the motion of the system.

25x

2

C

%

3.92x

C

#

0.576 " 0

 

1

2

 

(50)x

2

C

#

1

2

 

(0.80)(1.2)

2

" #

3.92x

C

!

E

mech

"

E

f

#

E

i

"

(0 %

1

2

 

kx

2

C

) # (

1

2

 

mv

2

A

%

0) " #

 

f

k

x

C

!

E

mech

" #

 

f

k

x

C

"

(#

 

3.92x

C

)

f

k

"

)

k

n " )

k

mg " 0.50(0.80 kg)(9.80 m/s

2

) " 3.92 N

0.15 m

x

max

"

√

m

k

 v

A

"

√

0.80 kg

50 N/m

 (1.2 m/s)

0 %

1

2

 

kx

2

max

"

1

2

 

mv

2

A

%

0

K

C

%

U

s

C

"

K

A

%

U

s

A

E

C

"

E

A

1

2

kx

2

"

1

2

kx

2

max

E = – mv

A

2

1

2

x = 0

(a)

(b)

(c)

v

C

 = 0

(d)

x

max

!

"

#

$

E = – mv

B

2

 + – kx

B

2

1

2

1

2

E = – mv

D

2

 = – mv

A

2

1

2

1

2

E = – kx

max

1

2

v

A

v

B

x

B

v

D

 = –v

A

2

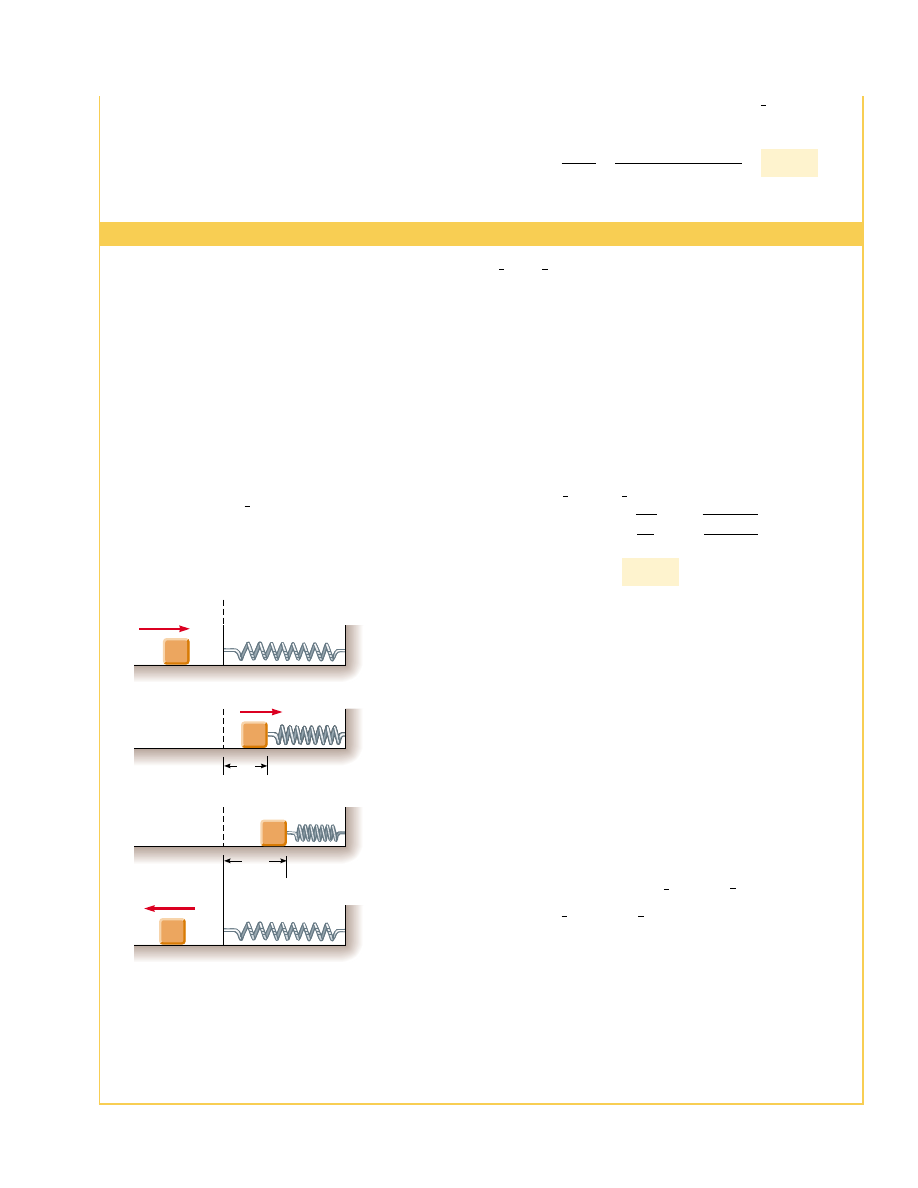
Figure 8.14 (Example 8.9) A block sliding on a smooth, hori-

zontal surface collides with a light spring. (a) Initially the me-

chanical energy is all kinetic energy. (b) The mechanical energy

is the sum of the kinetic energy of the block and the elastic po-

tential energy in the spring. (c) The energy is entirely potential

energy. (d) The energy is transformed back to the kinetic en-

ergy of the block. The total energy of the system remains con-

stant throughout the motion.

234

CHAPTE R 8 •  Potential Energy

8.5 Relationship Between Conservative Forces

and Potential Energy

In an earlier section we found that the work done on a member of a system by a conserv-
ative  force  between  the  members  does  not  depend  on  the  path  taken  by  the  moving
member. The work depends only on the initial and final coordinates. As a consequence,
we can define a 

potential energy function U such that the work done by a conservative

force equals the decrease in the potential energy of the system. Let us imagine a system
of particles in which the configuration changes due to the motion of one particle along
the x axis. The work done by a conservative force 

F as a particle moves along the x axis is

2

Example 8.10 Connected Blocks in Motion

Two blocks are connected by a light string that passes over a
frictionless  pulley,  as  shown  in  Figure  8.15.  The  block  of
mass m

1

lies  on  a  horizontal  surface  and  is  connected  to  a

spring of force constant k. The system is released from rest
when the spring is unstretched. If the hanging block of mass
m

2

falls a distance h before coming to rest, calculate the co-

efficient  of  kinetic  friction  between  the  block  of  mass  m

1

and the surface.

Solution The  key  word  rest appears  twice  in  the  problem
statement.  This  suggests  that  the  configurations  associated
with rest are good candidates for the initial and final config-
urations because the kinetic energy of the system is zero for
these  configurations.  (Also  note  that  because  we  are  con-
cerned  only  with  the  beginning  and  ending  points  of  the
motion, we do not need to label events with circled letters as
we did in the previous two examples. Simply using i and f is
sufficient  to  keep  track  of  the  situation.)  In  this  situation,
the  system  consists  of  the  two  blocks,  the  spring,  and  the
Earth.  We  need  to  consider  two  forms  of  potential  energy:
gravitational and elastic. Because the initial and final kinetic
energies of the system are zero, !K " 0, and we can write

where !U

g

"

U

g f

#

U

gi

is the change in the system’s gravitati-

onal potential energy and !U

s

"

U

sf

#

U

si

is the change in the

system’s elastic potential energy. As the hanging block falls a
distance h, the horizontally moving block moves the same dis-
tance h to the right. Therefore, using Equation 8.14, we find
that the loss in mechanical energy in the system due to friction
between the horizontally sliding block and the surface is

The change in the gravitational potential energy of the sys-
tem is associated with only the falling block because the ver-
tical  coordinate  of  the  horizontally  sliding  block  does  not
change. Therefore, we obtain

where the coordinates have been measured from the lowest
position of the falling block.

(3)

            !U

g

"

U

g f

#

U

g i

"

0 # m

2

gh

(2)

            !E

mech

" #

f

k

h " #

 

)

k

m

1

gh

   

(1)

            !E

mech

" !

U

g

% !

U

s

   

The change in the elastic potential energy of the system

is that stored in the spring:

Substituting  Equations  (2),  (3),  and  (4)  into  Equation  (1)
gives

This setup represents a way of measuring the coefficient

of  kinetic  friction  between  an  object  and  some  surface.  As
you can see from the problem, sometimes it is easier to work
with the changes in the various types of energy rather than
the actual values. For example, if we wanted to calculate the
numerical value of the gravitational potential energy associ-
ated  with  the  horizontally  sliding  block,  we  would  need  to
specify  the  height  of  the  horizontal  surface  relative  to  the
lowest  position  of  the  falling  block.  Fortunately,  this  is  not
necessary  because  the  gravitational  potential  energy  associ-
ated with the first block does not change.

)

k

"

m

2

g #

1

2

 

kh

m

1

g

#

)

k

m

1

gh " #

 

m

2

gh %

1

2

 

kh

2

(4)

            !U

s

"

U

sf

#

U

si

"

1

2

 

kh

2

#

0

 

k

h

m

1

m

2

Figure 8.15 (Example 8.10) As the hanging block moves from

its highest elevation to its lowest, the system loses gravitational

potential energy but gains elastic potential energy in the spring.

Some mechanical energy is lost because of friction between the

sliding block and the surface.

2

For  a  general  displacement,  the  work  done  in  two  or  three  dimensions  also  equals # !U,

where U " U(x, y, z). We write this formally as W " %

f

i  

F ! d r " U

i

#

U

f

.

SECTION 8.5 •  Relationship between Conservative Forces and Potential Energy

235

(8.15)

where F

x

is the component of 

F in the direction of the displacement. That is, the work

done by a conservative force acting between members of a system equals the negative
of the change in the potential energy associated with that force when the configuration
of  the  system  changes,  where  the  change  in  the  potential  energy  is  defined  as 
!

U " U

f

#

U

i

. We can also express Equation 8.15 as

(8.16)

Therefore, !U is negative when F

x

and dx are in the same direction, as when an object is

lowered in a gravitational field or when a spring pushes an object toward equilibrium.

The term potential energy implies that the system has the potential, or capability, of

either gaining kinetic energy or doing work when it is released under the influence of
a conservative force exerted on an object by some other member of the system. It is of-
ten convenient to establish some particular location x

i

of one member of a system as

representing  a  reference  configuration  and  measure  all  potential  energy  differences
with respect to it. We can then define the potential energy function as

(8.17)

The  value  of  U

i

is  often  taken  to  be  zero  for  the  reference  configuration.  It  really

does not matter what value we assign to U

i

because any nonzero value merely shifts U

f

(x)

by a constant amount and only the change in potential energy is physically meaningful.

If the conservative force is known as a function of position, we can use Equation

8.17 to calculate the change in potential energy of a system as an object within the sys-
tem moves from x

i

to x

f

.

If  the  point  of  application  of  the  force  undergoes  an  infinitesimal  displacement

dx, we can express the infinitesimal change in the potential energy of the system dU as

Therefore, the conservative force is related to the potential energy function through
the relationship

3

(8.18)

That is, 

the x component of a conservative force acting on an object within a sys-

tem equals the negative derivative of the potential energy of the system with re-
spect to x.

We can easily check this relationship for the two examples already discussed. In the

case of the deformed spring, 

, and therefore

which  corresponds  to  the  restoring  force  in  the  spring  (Hooke’s  law).  Because  the
gravitational potential energy function is U

g

"

mgy, it follows from Equation 8.18 that

F

g

" #

mg when we differentiate U

g

with respect to y instead of x.

We now see that U is an important function because a conservative force can be de-

rived from it. Furthermore, Equation 8.18 should clarify the fact that adding a constant
to the potential energy is unimportant because the derivative of a constant is zero.

F

s

" #

dU

s

dx

" #

d

dx

 (

1

2

 

kx

2

) " #kx

U

s

"

1

2

kx

2

 F

x

" #

dU

dx

dU " # F

x

 

 

dx

U

f

  

(x) " #

%

x

f

x

i

F

x

 

 

dx % U

i

!

U " U

f

#

U

i

" #

 

%

x

f

x

i

F

x

 

 

dx

W

c

"

%

x

f

x

i

F

x

 

 

dx " #

 

!

U

3

In three dimensions, the expression is, 

where 

etc. are partial

derivatives. In the language of vector calculus, 

F equals the negative of the gradient of the scalar quan-

tity U(x, y, z).

*

U

*

x

F " #

*

U

*

x

 

iˆ  #

*

U

*

y

 

jˆ  #

*

U

*

z

 

kˆ 

Relation of force between mem-

bers of a system to the potential

energy of the system

236

CHAPTE R 8 •  Potential Energy

8.6 Energy Diagrams and Equilibrium of a System

The motion of a system can often be understood qualitatively through a graph of its po-
tential energy versus the position of a member of the system. Consider the potential en-
ergy function for a block–spring system, given by 

. This function is plotted ver-

sus x in Figure 8.16a. (A common mistake is to think that potential energy on the graph
represents  height.  This  is  clearly  not  the  case  here,  where  the  block  is  only  moving
horizontally.)  The  force  F

s

exerted  by  the  spring  on  the  block  is  related  to  U

s

through

Equation 8.18:

As we saw in Quick Quiz 8.11, the x component of the force is equal to the negative of
the slope of the U-versus-x curve. When the block is placed at rest at the equilibrium
position of the spring (x " 0), where F

s

"

0, it will remain there unless some external

force  F

ext

acts  on  it.  If  this  external  force  stretches  the  spring  from  equilibrium,  x is

positive and the slope dU/dx is positive; therefore, the force F

s

exerted by the spring is

negative  and  the  block  accelerates  back  toward  x " 0  when  released.  If  the  external
force compresses the spring, then x is negative and the slope is negative; therefore, F

s

is

positive and again the mass accelerates toward x " 0 upon release.

From this analysis, we conclude that the x " 0 position for a block–spring system is

one of 

stable equilibrium. That is, any movement away from this position results in a

force directed back toward x " 0. In general, 

configurations of stable equilibrium

correspond to those for which U(x) is a minimum.

From Figure 8.16 we see that if the block is given an initial displacement x

max

and is

released from rest, its total energy initially is the potential energy 

stored in the

1

2

kx

2

max

 F

s

" #

dU

s

dx

" #

 

kx

U

s

"

1

2

kx

2

Quick Quiz 8.11

What does the slope of a graph of U(x) versus x represent?

(a) the magnitude of the force on the object (b) the negative of the magnitude of the
force on the object (c) the x component of the force on the object (d) the negative of
the x component of the force on the object.

E

–x

max

0

U

s

x

(a)

x

max

(b)

m

x = 0

= – kx

2

1

2

U

s

x

max

F

s

Active Figure 8.16 (a) Potential energy as

a function of x for the frictionless

block–spring system shown in (b). The

block oscillates between the turning points,

which have the coordinates x " + x

max

.

Note that the restoring force exerted by

the spring always acts toward x " 0, the

position of stable equilibrium.

Stable equilibrium

At the Active Figures

link at http://www.pse6.com,
you can observe the block
oscillate between its turning
points and trace the
corresponding points on the
potential energy curve for
varying values of k.