Physics For Scientists And Engineers 6E - part 17

Multiplying a Vector by a Scalar

If vector 

A is multiplied by a positive scalar quantity m, then the product mA is a vector

that has the same direction as 

A and magnitude mA. If vector A is multiplied by a nega-

tive scalar quantity # m, then the product # m

A is directed opposite A. For example,

the vector 5

A is five times as long as A and points in the same direction as A; the vector

is one-third the length of 

A and points in the direction opposite A.

3.4 Components of a Vector and Unit Vectors

The graphical method of adding vectors is not recommended whenever high accuracy
is required or in three-dimensional problems. In this section, we describe a method of
adding  vectors  that  makes  use  of  the  projections  of  vectors  along  coordinate  axes.
These  projections  are  called  the 

components of  the  vector.  Any  vector  can  be  com-

pletely described by its components.

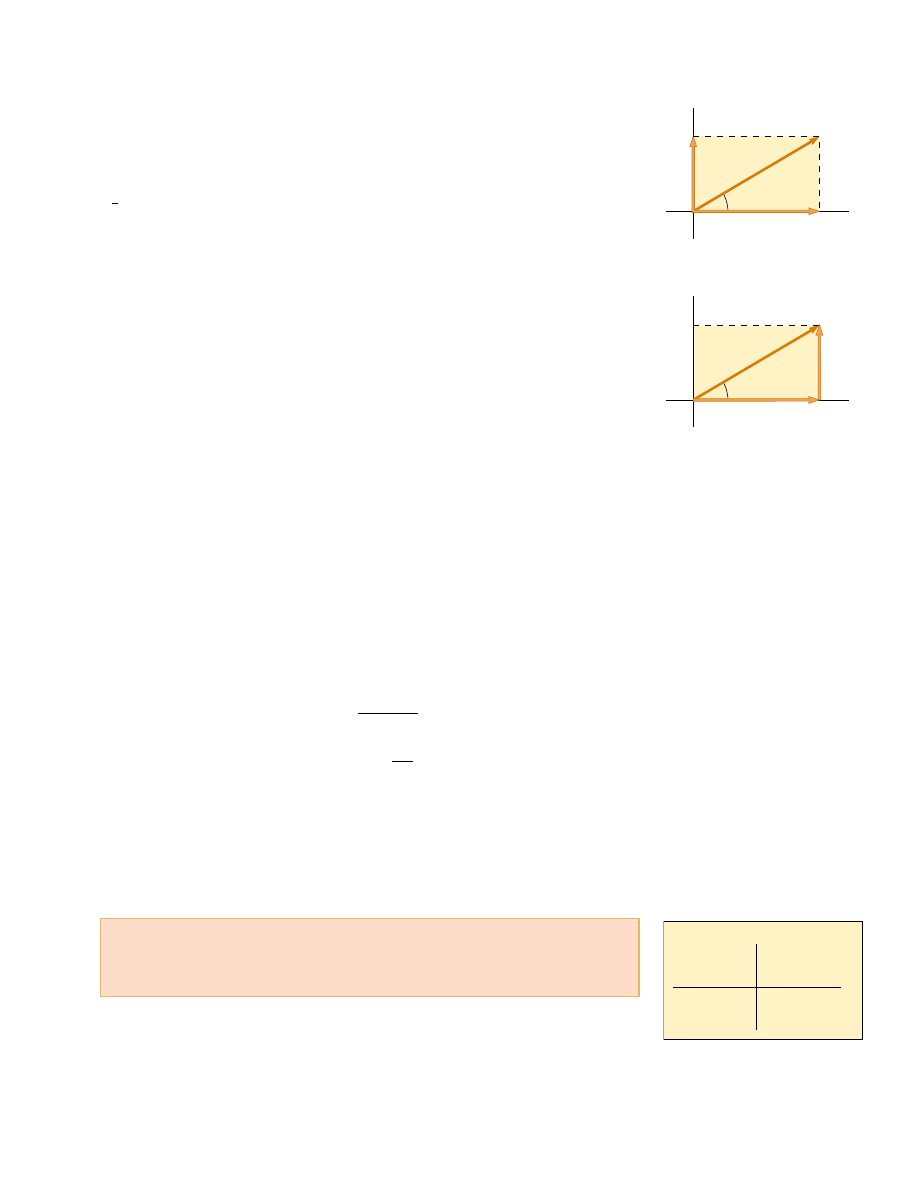
Consider a vector 

A lying in the xy plane and making an arbitrary angle ! with the

positive x axis, as shown in Figure 3.13a. This vector can be expressed as the sum of two
other vectors 

A

x

and 

A

y

. From Figure 3.13b, we see that the three vectors form a right

triangle and that 

A " A

x

%

A

y

. We shall often refer to the “components of a vector 

A,”

written A

x

and A

y

(without the boldface notation). The component A

x

represents the

projection of 

A along the x axis, and the component A

y

represents the projection of 

A

along the y axis. These components can be positive or negative. The component A

x

is

positive if 

A

x

points in the positive x direction and is negative if 

A

x

points in the nega-

tive x direction. The same is true for the component A

y

.

From Figure 3.13 and the definition of sine and cosine, we see that cos ! "

A

x

/A

and that sin ! "

A

y

/A. Hence, the components of 

A are

(3.8)

(3.9)

These  components  form  two  sides  of  a  right  triangle  with  a  hypotenuse  of  length  A.
Thus, it follows that the magnitude and direction of 

A are related to its components

through the expressions

(3.10)

(3.11)

Note that 

the signs of the components A

x

and A

y

depend on the angle !. For

example, if ! " 120°, then 

A

x

is negative and A

y

is positive. If ! " 225°, then both A

x

and A

y

are negative. Figure 3.14 summarizes the signs of the components when 

A lies

in the various quadrants.

When solving problems, you can specify a vector 

A either with its components A

x

and A

y

or with its magnitude and direction A and !.

! "

tan

#

1 

"

A

y

A

x

#

A "

√

A

x

 

2

%

A

y

 

2

A

y

"

A sin !

A

x

"

A cos !

#

1

3

A

SECTION 3.4 •  Components of a Vector and Unit Vectors

65

y

x

A

O

A

y

A

x

θ

(a)

y

x

A

O

A

x

θ

(b)

A

y

Figure 3.13 (a) A vector A lying in

the xy plane can be represented by

its component vectors A

x

and A

y

.

(b) The y component vector A

y

can

be moved to the right so that it

adds to A

x

. The vector sum of the

component vectors is A. These

three vectors form a right triangle.

▲

PITFALL PREVENTION

3.2 Component Vectors

versus Components

The  vectors  A

x

and  A

y

are  the

component  vectors of  A.  These
should  not  be  confused  with  the
scalars A

x

and A

y

, which we shall

always  refer  to  as  the  components
of A.

Quick Quiz 3.5

Choose the correct response to make the sentence true: A

component of a vector is (a) always, (b) never, or (c) sometimes larger than the magni-
tude of the vector.

y

x

A

x

  

positive

A

y

  

positive

A

x

  

positive

A

y

  

negative

A

x

  

negative

A

y 

 

positive

A

x

  

negative

A

y

  

negative

Figure 3.14 The signs of the com-

ponents of a vector A depend on

the quadrant in which the vector is

located.

Components of the vector A

Suppose you are working a physics problem that requires resolving a vector into its

components. In many applications it is convenient to express the components in a co-
ordinate system having axes that are not horizontal and vertical but are still perpendic-
ular to each other. If you choose reference axes or an angle other than the axes and
angle shown in Figure 3.13, the components must be modified accordingly. Suppose a

vector 

B makes an angle !( with the x( axis defined in Figure 3.15. The components of

B along the x( and y( axes are B

x(

"

B cos !( and B

y(

"

B sin !(, as specified by Equa-

tions  3.8  and  3.9.  The  magnitude  and  direction  of 

B are  obtained  from  expressions

equivalent  to  Equations  3.10  and  3.11.  Thus,  we  can  express  the  components  of  a
vector in any coordinate system that is convenient for a particular situation.

Unit Vectors

Vector quantities often are expressed in terms of unit vectors. 

A unit vector is a dimen-

sionless  vector  having  a  magnitude  of  exactly  1. Unit vectors are used to specify a
given direction and have no other physical significance. They are used solely as a conve-
nience in describing a direction in space. We shall use the symbols ˆ

i , ˆj, and ˆk to repre-

sent unit vectors pointing in the positive x, y, and z directions, respectively. (The “hats” on
the symbols are a standard notation for unit vectors.) The unit vectors ˆ

i , ˆj, and ˆk form a

set of mutually perpendicular vectors in a right-handed coordinate system, as shown in
Figure 3.16a. The magnitude of each unit vector equals 1; that is, 

!ˆi! = !ˆj! = ! ˆk! = 1.

Consider a vector 

A lying in the xy plane, as shown in Figure 3.16b. The product

of the component A

x

and the unit vector ˆ

i is the vector A

x

ˆi, which lies on the x axis

and  has  magnitude 

!A

x

!. (The vector A

x

ˆi is an alternative representation of vector

A

x

.) Likewise, A

y

ˆj is a vector of magnitude !A

y

! lying on the y axis. (Again, vector A

y

ˆj

is an alternative representation of vector 

A

y

.) Thus, the unit–vector notation for the

vector 

A is

A " A

x

ˆi % A

y

ˆj

(3.12)

For example, consider a point lying in the xy plane and having Cartesian coordinates
(x, y), as in Figure 3.17. The point can be specified by the 

position vector r, which in

unit–vector form is given by

r " xˆi % yˆj

(3.13)

This notation tells us that the components of 

r are the lengths x and y.

Now let us see how to use components to add vectors when the graphical method is

not sufficiently accurate. Suppose we wish to add vector 

B to vector A in Equation 3.12,

where vector 

B has components B

x

and B

y

. All we do is add the x and y components

separately. The resultant vector 

R " A % B is therefore

R " (A

x

ˆi % A

y

ˆj) % (B

x

ˆi % B

y

ˆj)

or

R " (A

x

%

B

x

)ˆ

i % (A

y

%

B

y

)ˆ

j

(3.14)

Because 

R " R

x

ˆi % R

y

ˆj, we see that the components of the resultant vector are

R

x

"

A

x

%

B

x

R

y

"

A

y

%

B

y

(3.15)

66

CHAPTE R 3 •  Vectors

Active Figure 3.16 (a) The unit
vectors ˆi, ˆj, and ˆk are directed
along the x, y, and z axes, respec-
tively. (b) Vector A " A

x

ˆi % A

y

ˆj ly-

ing in the xy plane has components
A

x

and A

y

. 

x

y

z

(a)

y

x

(b)

A

jˆ

iˆ

kˆ

A

y

jˆ

A

x

iˆ

y

x

O

r

(x,y)

Figure 3.17 The point whose Cartesian coordinates 
are (x, y) can be represented by the position vector 
r " xˆi % yˆj.

Figure 3.15 The component vec-

tors of B in a coordinate system

that is tilted.

x

′

y

′

B

B

y

′

B

x

′

O

θ

′

At the Active Figures link

at http://www.pse6.com you

can rotate the coordinate axes

in 3-dimensional space and

view a representation of vector

A in three dimensions.

P R O B L E M - S O LV I N G   H I N T S

Adding Vectors

When you need to add two or more vectors, use this step-by-step procedure:

•

Select a coordinate system that is convenient. (Try to reduce the number of
components you need to calculate by choosing axes that line up with as many
vectors as possible.)

•

Draw a labeled sketch of the vectors described in the problem.

•

Find the x and y components of all vectors and the resultant components (the
algebraic sum of the components) in the x and y directions.

•

If necessary, use the Pythagorean theorem to find the magnitude of the
resultant vector and select a suitable trigonometric function to find the angle
that the resultant vector makes with the x axis.

We obtain the magnitude of 

R and the angle it makes with the x axis from its compo-

nents, using the relationships

(3.16)

(3.17)

We can check this addition by components with a geometric construction, as shown

in Figure 3.18. Remember that you must note the signs of the components when using
either the algebraic or the graphical method.

At times, we need to consider situations involving motion in three component direc-

tions. The extension of our methods to three-dimensional vectors is straightforward. If
A and B both have x, y, and z components, we express them in the form

A " A

x

ˆi % A

y

ˆj % A

z

ˆk

(3.18)

B " B

x

ˆi % B

y

ˆj % B

z

ˆk

(3.19)

The sum of 

A and B is

R " (A

x

%

B

x

)ˆ

i % (A

y

%

B

y

)ˆ

j % (A

z

%

B

z

)ˆ

k

(3.20)

Note that Equation 3.20 differs from Equation 3.14: in Equation 3.20, the resultant vec-
tor also has a z component R

z

"

A

z

%

B

z

. If a vector 

R has x, y, and z components, the 

magnitude of the vector is 

. The angle !

x

that 

R makes with the

x axis is found from the expression cos !

x

"

R

x

/R, with similar expressions for the an-

gles with respect to the y and z axes.

 R "

√

R

2

x

%

R

2

y

%

R

2

z  

tan

 

! "

R

y

R

x

"

A

y

%

B

y

A

x

%

B

x

R "

√

R

x

 

2

%

R

y

 

2

"

√

(A

x

%

B

x

)

2

%

(A

y

%

B

y

)

2

SECTION 3.4 •  Components of a Vector and Unit Vectors

67

Quick Quiz 3.6

If at least one component of a vector is a positive number,

the vector cannot (a) have any component that is negative (b) be zero (c) have three
dimensions.

Quick Quiz 3.7

If A % B " 0, the corresponding components of the two vec-

tors A and B must be (a) equal (b) positive (c) negative (d) of opposite sign.

Quick  Quiz  3.8

For  which  of  the  following  vectors  is  the  magnitude  of  the

vector  equal  to  one  of  the  components  of  the  vector?  (a)  A " 2iˆ % 5ˆj (b)  B " # 3ˆj
(c) C " % 5 kˆ

Figure 3.18 This geometric con-

struction for the sum of two vectors

shows the relationship between the

components of the resultant R and

the components of the individual

vectors.

y

R

B

A

x

B

x

A

y

A

x

R

x

B

y

R

y

▲

PITFALL PREVENTION

3.4 Tangents on

Calculators

Generally,  the  inverse  tangent
function  on  calculators  provides
an  angle  between  # 90° and 
%

90°.  As  a  consequence,  if  the

vector you are studying lies in the
second or third quadrant, the an-
gle measured from the positive x
axis will be the angle your calcu-
lator returns plus 180°.

▲

PITFALL PREVENTION

3.3 x and y Components

Equations  3.8  and  3.9  associate
the cosine of the angle with the x
component  and  the  sine  of  the
angle with the y component. This
is true only because we measured
the angle ! with respect to the x
axis,  so  don’t  memorize  these
equations.  If  ! is  measured  with
respect  to  the  y axis  (as  in  some
problems),  these  equations  will
be  incorrect.  Think  about  which
side  of  the  triangle  containing
the  components  is  adjacent  to
the angle and which side is oppo-
site,  and  assign  the  cosine  and
sine accordingly.

68

CHAPTE R 3 •  Vectors

Example 3.4 The Resultant Displacement

A  particle  undergoes  three  consecutive  displacements:

d

1

"

(15ˆ

i % 30ˆj % 12 ˆk) cm,  d

2

"

(23ˆ

i # 14ˆj # 5.0 ˆk) cm

and 

d

3

"

(# 13ˆ

i % 15ˆj) cm.  Find  the  components  of  the

resultant displacement and its magnitude.

Solution Three-dimensional  displacements  are  more  diffi-
cult  to  imagine  than  those  in  two  dimensions,  because  the
latter can be drawn on paper. For this problem, let us concep-
tualize that you start with your pencil at the origin of a piece
of graph paper on which you have drawn x and y axes. Move
your pencil 15 cm to the right along the x axis, then 30 cm
upward along the y axis, and then 12 cm vertically away from
the graph paper. This provides the displacement described
by 

d

1

. From this point, move your pencil 23 cm to the right

parallel to the x axis, 14 cm parallel to the graph paper in
the  # y direction,  and  then  5.0 cm  vertically  downward  to-
ward  the  graph  paper.  You  are  now  at  the  displacement
from the origin described by 

d

1

%

d

2

. From this point, move

your  pencil  13 cm  to  the  left  in  the  # x direction,  and  (fi-
nally!)  15 cm  parallel  to  the  graph  paper  along  the  y axis.

Your  final  position  is  at  a  displacement 

d

1

%

d

2

%

d

3

from

the origin.

Despite the difficulty in conceptualizing in three dimen-

sions, we can categorize this problem as a plug-in problem due
to the careful bookkeeping methods that we have developed
for  vectors.  The  mathematical  manipulation  keeps  track  of
this  motion  along  the  three  perpendicular  axes  in  an  orga-
nized, compact way:

R " d

1

%

d

2

%

d

3

"

(15 % 23 # 13)ˆ

i cm % (30 # 14 % 15)ˆj cm

%

(12 # 5.0 % 0)ˆ

k cm

"

(25ˆ

i % 31ˆj % 7.0ˆk) cm

The  resultant  displacement  has  components  R

x

"

25 cm,

R

y

"

31 cm, and R

z

"

7.0 cm. Its magnitude is

40 cm

"

√

(25 cm)

2

%

(31 cm)

2

%

(7.0 cm)

2

  "

R  "

√

R

x

2

%

R

y

2

%

R

z

2

Example 3.3 The Sum of Two Vectors

Find  the  sum  of  two  vectors 

A and B lying in the xy plane

and given by

A " (2.0ˆi % 2.0ˆj) m

and

B " (2.0ˆi # 4.0ˆj) m

Solution You  may  wish  to  draw  the  vectors  to  conceptualize
the situation. We categorize this as a simple plug-in problem.
Comparing  this  expression  for 

A with  the  general  expres-

sion 

A " A

x

ˆi % A

y

ˆj, we see that A

x

"

2.0 m and A

y

"

2.0 m.

Likewise, B

x

"

2.0 m and B

y

" #

4.0 m. We obtain the resul-

tant vector 

R, using Equation 3.14:

R " A % B " (2.0 % 2.0)ˆi m % (2.0 # 4.0)ˆj m

"

(4.0ˆ

i # 2.0ˆj) m

or

R

x

"

4.0 m

R

y

" #

2.0 m

The magnitude of 

R is found using Equation 3.16:

We can find the direction of 

R from Equation 3.17:

Your  calculator  likely  gives  the  answer  # 27° for  ! "
tan

#

1

(# 0.50).  This  answer  is  correct  if  we  interpret  it  to

mean 27° clockwise from the x axis. Our standard form has
been  to  quote  the  angles  measured  counterclockwise  from 

the % x axis, and that angle for this vector is   ! " 333° .

tan

 

! "

R

y

R

x

"

#

2.0 m

4.0 m

" #

0.50

4.5 m

"

 

R  "

√

R

x

2

%

R

y

2

"

√

(4.0 m)

2

%

(#2.0 m)

2

"

√

20 m

Example 3.5 Taking a Hike

A hiker begins a trip by first walking 25.0 km southeast from
her car. She stops and sets up her tent for the night. On the
second day, she walks 40.0 km in a direction 60.0° north of
east, at which point she discovers a forest ranger’s tower.

(A)

Determine the components of the hiker’s displacement

for each day.

Solution We conceptualize the problem by drawing a sketch as
in Figure 3.19. If we denote the displacement vectors on the
first and second days by 

A and B, respectively, and use the car

as  the  origin  of  coordinates,  we  obtain  the  vectors  shown  in
Figure 3.19. Drawing the resultant 

R, we can now categorize this

as a problem we’ve solved before—an addition of two vectors.
This should give you a hint of the power of categorization—
many new problems are very similar to problems that we have
already solved if we are careful to conceptualize them.

We will analyze this problem by using our new knowledge

of vector components. Displacement 

A has a magnitude of

25.0 km and is directed 45.0° below the positive x axis. From
Equations 3.8 and 3.9, its components are

The negative value of A

y

indicates that the hiker walks in the

negative y direction on the first day. The signs of A

x

and A

y

also are evident from Figure 3.19.

The second displacement 

B has a magnitude of 40.0 km

and is 60.0° north of east. Its components are

#

17.7 km

A

y

"

A sin(#45.0$) " (25.0 km)(#0.707) "

17.7 km

A

x

"

A cos (#45.0$) " (25.0 km)(0.707) "

Interactive