Телеграфные службы, сети и службы ПД - часть 3

привело   к   их   широкому   использованию   в   УЗО.   Для   систе-

матического кода применяется обозначение  (п,k) —  код, где

п   —  число   элементов   в   комбинации;  k  —  число   инфор-

мационных элементов.

Характерной особенностью этих кодов является также и то,

что информационные и проверочные элементы связаны между

собой   зависимостями,   описываемыми   линейными   уравнения-

ми.   Отсюда   возникает   и   второе   название   систематических

кодов — линейные.

Код Хемминга. Рассмотрим в качестве примера построение

систематического   кода   с   кодовым   расстоянием  do  =   3  (кода
Хемминга).  Пусть  число   сообщений,   которое   необходимо  пе-
редать,   равно   16.   Тогда   необходимое   число   информационных
элементов k = log

2

N

a

 = 4. Можно выписать все 16 кодовых

комбинаций, включая нулевую (0000). Это один из возможных

способов   задания   исходного   (простого)   кода.   Другой   способ

заключается   в   выписывании   только   четырех   кодовых   ком-

бинаций   простого   кода   в   виде   матрицы,   называемой   еди-

ничной:

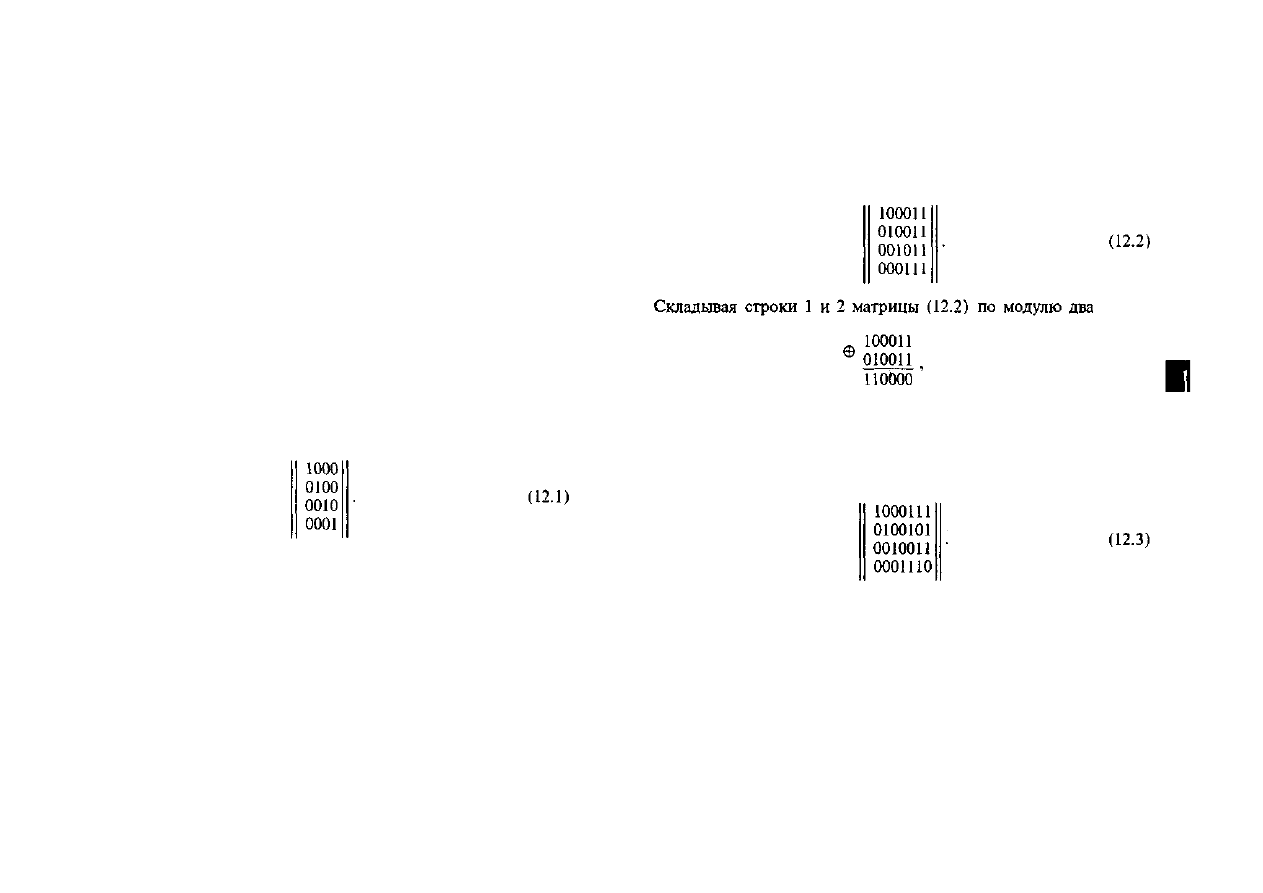
Суммируя по модулю два в различном сочетании кодовые

комбинации, входящие в единичную матрицу, можно получить
15   кодовых   комбинаций,   16-я   —   нулевая.   Кодовые   ком-
бинации,   составляющие   матрицу   (12.1),   линейно   независимы.
Можно   было   бы   составить   матрицу   и   из   других   кодовых
комбинаций   (лишь   бы   они   были   линейно   независимыми).
Ненулевые   комбинации  А

1

,   А

2

,  Л

3

,  А

4

  линейно   независимые,

если q

1

A

1

 

 

 q

2

A

2



 q

3

А

3

 



 q

4

A

4

 ≠ 0, где qi 



 {0,1} при

условии,   что   хотя   бы   один   из   коэффициентов  qi  ≠  0.   До-
полним   каждую   кодовую   комбинацию   в   (12.1)   проверочными
элементами так, чтобы обеспечивалось do = 3. Будем иметь в
виду также тот факт, что к числу разрешенных комбинаций
корректирующего кода принадлежит и комбинация 0000 ... 0,

называемая  нулевой.  Очевидно, что в числе добавляемых про-

верочных элементов должно быть не менее двух единиц. Тогда

общее  число  единиц  в каждой комбинации  кода  получим  не

меньше трех и комбинации, полученные нами, будут отличать-

ся от нулевой, по крайней мере, в трех элементах. Добавим по

две единицы к каждой строке матрицы (12.1):

видим,   что   они   отличаются   только   в   двух   элементах,   т.е.

заданное   кодовое   расстояние   не   обеспечивается.   Дополним

каждую строку проверочными элементами так, чтобы do = 3.
Тогда матрица примет вид

Добавляемые проверочные элементы могут быть записаны и в

другом порядке. Необходимо лишь обеспечить do = 3.

Матрицу (12.3) называют производящей, или  порождающей,

матрицей кода (7,4), содержащего семь элементов, из которых

четыре информационных. Обычно матрицу обозначают буквой

G  с индексом, указывающим, к какому коду она относится (в

нашем случае G

(7,4)

). Производящая матрица состоит из двух

матриц — единичной (размерности k • k ) и С

(r,k)

 , 

содержащей r  столбцов и k строк. Суммируя в различном 
сочетании строки матрицы (12.3), получаем все (кроме нулевой) 
комбинации корректирующего кода с do = 3.

Единицы, расположенные на местах, соответствующих ин-

формационным элементам матрицы Н

(7,4)

, указывают на то,

какие информационные элементы должны участвовать в фор-

мировании проверочного элемента. Единица на месте, соответ-

ствующем проверочному элементу, указывает, какой провероч-

ный элемент получается при суммировании по модулю два

Комбинация  b

3

b

2

b

1

  называется   синдромом   (проверочным

вектором). Равенство нулю всех элементов синдрома указывает

на отсутствие ошибок, или на то, что кодовая комбинация

принята с ошибками, которые превратили ее в другую разре-

шенную.   Последнее   событие   имеет   существенно   меньшую

вероятность, чем первое.

Вид ненулевого синдрома определяется характером ошибок

в кодовой комбинации. В нашем случае вид синдрома зависит

от местоположения одиночной ошибки. В табл. 12.2 отражено

соответствие между местоположением одиночной ошибки для

кода, заданного матрицей (12.3), и видом синдрома.

Таким   образом,  зная  вид   синдрома,   можно   определить

место, где произошла ошибка, и исправить принятый элемент

на противоположный.

Деление выполняется как обычно, только вычитание заме-

няется суммированием по модулю два.

Разрешенные   комбинации   циклического   кода   обладают

двумя   очень   важными   отличительными   признаками:   цикли-

ческий сдвиг разрешенной комбинации тоже приводит к раз-

решенной   кодовой   комбинации.   Все   разрешенные   кодовые

комбинации делятся без остатка на полином  Р(х),  называемый

образующим.  Эти свойства используются при построении цик-

лических кодов, кодирующих и декодирующих устройств, а

также при обнаружении и исправлении ошибок.

Найдем   алгоритмы   построения   циклического   кода,   удов-

летворяющего перечисленным выше условиям. Задан полином

1

...

)

(

1

2

1















r

r

r

r

x

a

x

a

x

P

,   определяющий   корректи-

рующую   способность   кода,   и   задан   исходный   простой   код,

который   требуется   преобразовать   в   корректирующий   цик-

лический.

Перепишем равенство (12.11) в виде

G(x)P(x) = Q(x)x

r

 + R(x).

(12.12)

Левая часть (12.12) делится без остатка на  Р(х),  значит без

остатка   делится   и   правая   часть.   Из   (12.12)   вытекают   два

способа формирования комбинаций циклического кода: путем

умножения многочлена G(x) на Р(х) и путем деления Q(x)x

r

на Р(х) и приписывания к Q(x)x

r

 остатка от деления R(x).

Пример 12.5.  Задан полином  G(x) =  х

3

  + х, соответству-

ющий   комбинации   простого   кода.   Сформируем   комбинацию

циклического кода (7,4) с производящим полиномом Р(х) =

= х

3

  + х

2

  +  1. Можно получить комбинацию циклического

кода в виде G(x)P(x) = (х

3

 + х) (х

3

 + х

2

 + 1) = х

6

 + х

5

 + +

х

4

  +   х.   Однако   в   полученной   комбинации   нельзя   отделить

информационные элементы от проверочных, и код получается

неразделимым.

Перейдем ко второму способу, который чаще всего приме-

няется   на   практике.   Проделаем   необходимые   операции   по

получению комбинации циклического кода:

1) G(x)x

r

 = (х

3

 + х)х

3

 = х

6

 + х

4

;

2)

Х

6

+х

4

           I             

х  

3  

+х  

2

  

  

  +1

        

х

6

+х

5

+

х

3

     \х

3

+

х

2

+\

               х

5

+х

4

+х

3

               х

 

 

5

  +х*+х

 

 

2

  

                                         

 

 '

              х

3

+х

2

               

 

 х  

3

  +х

   

2

  +1

       

                 R(x)=1

3) (х

6

  + х

4

  + 1) — комбинация циклического кода, полу-

ченная   методом   деления   на   производящий   полином.   Она

может быть переписана в виде 1010001. Первые четыре элемен-

та   —   информационные,   последние   три   —   проверочные,   т.е.

полученный код — разделимый.

Для обнаружения ошибок в принятой кодовой комбинации

достаточно   поделить   ее   на   производящий   полином.   Если

принятая комбинация разрешенная, то остаток от деления

будет нулевым. Ненулевой остаток свидетельствует о том, что

принятая   комбинация   содержит   ошибки.   По   виду   остатка

(синдрома) можно в некоторых случаях также сделать вывод о

характере ошибки и исправить ее.

Циклические коды достаточно просты в реализации, обла-

дают   высокой   корректирующей   способностью   (способностью

исправлять и обнаруживать ошибки) и поэтому рекомендованы

МСЭ-Т для применения в аппаратуре ПД. Согласно рекомен-

дации V.41 в системах ПД с ОС рекомендуется применять код

с производящим полиномом Р(х) = х

16

 + х

12

 + х

5

 + 1.

Эффективность применения  корректирующих кодов.  Полезный

эффект от применения корректирующих кодов заключается в

повышении верности. Вероятность неправильного приема ко-

довой   комбинации  простого  кода  определяется   как   вероят-

ность   появления   в   кодовой   комбинации   хотя   бы   одной

ошибки, т.е.

где  р

ош

  —  вероятность   неправильного   приема   единичного

элемента;  k  —  число элементов в комбинации простого кода.

При   применении   систематических   корректирующих   кодов   к

исходной кодовой комбинации добавляются проверочные эле-

менты, позволяющие исправлять или обнаруживать ошибки.

Так, если код используется в режиме исправления ошибок и

кратность   исправляемых   ошибок  t

и.ош

,   то   вероятность   не-

правильного приема кодовой комбинации

В результате применения корректирующего кода в режиме

исправления ошибок вероятность ошибки уменьшается в  К

к

раз:  

)

(

)

(

/

И

ОШ

П

ОШ

и

Р

Р

K 

  >   1-   Однако   это   достигается   за   счет

увеличения затрат на реализацию системы и снижения ско-
рости передачи информации. Если в системе с простым кодом
скорость   равна   С

п

,   то   в   системе   с   корректирующим   кодом

скорость С

к

 = С

п

 • 

1



 где 

1



 = k/n — коэффициент, харак-